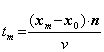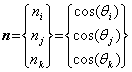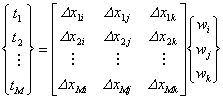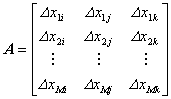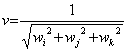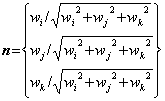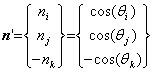最近の研究の紹介：木造住宅の崩壊解析による耐震診断−新しい精密・動的な耐震診断と補強方法−

木造の建売/注文住宅の崩壊解析による耐震診断法を開発。住まいの新しく精密で動的な耐震診断法であり、設計図から建物の欠陥を発見。シミュレーションで３次元（d3）アニメ動画表示。建設業者/メーカーによる耐震リフォーム/耐震補強/地震対策の費用を安く抑え、地震に強い一戸建て木造の新築/中古/建売/注文住宅の建設/家づくり/リフォーム/耐震改修を達成。

論文著者名：タイトル
（雑誌名）

土木学会論文集，No.780/I-70, pp.41-56, 2005

アレー観測データに基づく地表面近傍での地震波動の伝播方向の推定(3)
楊仲元，川上英二

２．理　論

 (1)  基準入力−出力最小化(NIOM)法5),6)

NIOM法は，波動伝播を多変数線形システムでモデル化し，波形相互の伝達関数を満足する簡単な形状の波形群を作成し，波動の伝播特性や空間変動特性などを調べるための方法である．

NIOM法は定常多変数線形システムの振動数領域での理論に基づいており，入力観測波形と出力観測波形 (のフーリエ変換，それぞれと (，を伝達関数で次式のように関係付けている．まず，伝達関数を観測波形と式(1)を用いて計算する．

                     (1)

   (; ;)

ただし，はサンプリング間隔，はサンプル数である．地震動でNS−EW−UDの３成分を考えると伝達関数は3×3の行列として考えることも可能ではあるが，本論文では３つの成分をそれぞれ別々に検討しており，伝達関数はスカラーとして考えている．

　伝達関数はシステムの物理的特性だけに依存するので，モデル化された入力と出力の間にも，観測波形と式(1)とから算定される伝達関数で結ばれる次の関係が成り立つものと仮定する．

               　   (2)

ただし，モデル化された入力と出力を，すなわち時間の関数としてのとを，また，それぞれのフーリエ変換であるとを，以降では，「入力モデル」と「出力モデル」と呼ぶことにする．ここで，モデル化とは，複雑な形状をした観測波形の組合せを，観測波形間の相互の関係を表す伝達関数は同一に保つが，簡単な（振幅が小さく継続時間が短い）波形の組合せに再表現することを意味している．

　ただし，一般にフィードバック・システムにおいては，入力と出力を分離して観測することは不可能であり，本論文における「入力」とは入射波を意味していない．任意の一地点（以下の解析ではボーリング孔C0の地表面）で観測された地震波動を「入力」と呼んでいる．

　入力モデルの離散フーリエ逆変換は次式で与えられる．                          

              (3)

ここで，任意の時刻で，例えばで，すなわちで，入力モデルの振幅は１に規準化されていると仮定すると，式(3)から次式が得られる．

                       　 (4)

　ラグランジェ未定係数法を用いて，入力モデルと出力モデルのフーリエ振幅の自乗和を式(4)の条件付きで最小化することを考える．ここで，フーリエ振幅の自乗和の小さな波形を求める理由は，振幅が小さく継続時間が短い波形，つまり単純な波形を求めるためである．ただし，複雑な観測波形の間と単純なモデルの間では伝達関数（すなわちフーリエ変換するとインパルス応答）は同一であり，波の反射や透過などに伴う変形を表す波形間の関係はモデル化に際して不変に保たれている．

また，入出力モデルを平滑化するため，とだけでなくこれらの時間微分であるとも考慮し，これらのフーリエ振幅スペクトルの自乗値の重み付き和を最小化する．まず，次の関数を考える．

　　  　 (5)

ただし，はラグランジェの乗数である．また，〜は１つの入力とM個の出力 (の重み係数であり，〜はこれらの時間微分の重み係数である．モデルの波形とそれを時間で微分した波形の重み係数の比が入力と出力に対して等しいものと考えると，重み係数は次式の関係を満足するものと設定できる．

              　　　　  (6)

また，入力と出力を対等に扱うことにすると，これらに対する重み係数であると (は全て１に設定できる．この場合，結局，重み係数としてはだけを与える必要があるが，を増加させることは入出力モデルの高振動数成分の振幅を減少させることに相当する5),6).着目したい振動数領域に応じて重み係数を設定する必要がある．

　入力モデルと出力モデルは式(5)を最小化することにより求められ，は式(2)(6)を式(5)に代入し，以下の条件により求められる．

         =0 　　　　    (7)

結局，入力モデルと出力モデルは次式で得られる5),6)．

                                                 (8)

                                                  (9)



ただし，伝達関数としては，観測波形と (のフーリエ変換，それぞれと (，を式(1)に代入することにより計算されたものを用いる．また，式(9)は式(8)で得られた単純化された入力モデルに対する線形システムの応答（式(2)参照）である．複雑な観測波形相互の関係を表す伝達関数（位相関係を含む）を満足するような単純な波形モデルの組合せ，と (，を求める本方法，そして，波動伝播状況を解析する本方法はNormalized Input-Output Minimization (NIOM)法5),6)と呼ばれている．入出力モデルは観測波形のスペクトルの形状の影響を受けず，この点が本手法の１つの特徴である．本論文では，NIOM法を用いて観測波形を単純にモデル化し，入射波や反射波の到達時刻の観測地点による違いを求め，これを基に地震動の伝播方向を算定している．

(2) 地震動伝播方向の推定方法

地盤内に，東，北，上の３方向それぞれをとおく座標系を考える．地点B0（基準点と呼ぶ）の位置ベクトルと地点Bmの位置ベクトル の間における地震波の伝達時間は次式で与えられる．

　　　                          (10)

ここで，は地震波動の伝播速度，「・」は内積である．は４章に示すように観測波形にNIOM法を適用することにより求められる．は伝播方向の単位ベクトルであり，座標軸となす角度をそれぞれとおくと，次式で表される．

                             (11)

式(10)を地点1〜Mに対してマトリクスを用いて示すと，次式が得られる．

            (12)

ただし

     (13)
              　　     (14)

である．ここで，

                                 (15)

                                          (16)

と置くと，式(12)は次式に書き換えられる．

                                                 (17)

本方程式の未知数はの3つ，式の数は観測地点の数（ただし，）である．自乗誤差を最小にするの解は，次式のように得られる8)．

                                   (18)

が求められると，式(14)より地震波動の伝播速度と伝播方向の単位ベクトルは次式のように得られる．

                      　  (19)

                      (20)

また，式(11)(20)より伝播方向を表す方位角は次式のように求められる．

               (21)

              (22)

              (23)

地中より地表面への入射波の伝播方向が式(11)(21)-(23)のように求められた場合には，反射波の伝播方向として，水平方向には同一方向であり，鉛直方向は逆方向である理論解を考えると，これは次式で表される．

              　       (24)

また，地震波動の伝播方向がで与えられる場合には，地震波動の到来方向はである．

波動の到達時刻の違いを利用して波動の伝播方向を求める本手法は，基本的にはセンブランス法などの従来の方法と同様な考えに基づくものである．しかし，提案手法では各地点の入射波・反射波それぞれに対しNIOM法に基づき伝達時間を先ず推定しており，これが本手法の特徴である．

本解析では式(10)に示すように，伝播速度が一定であることを仮定している．しかし，実際には地表面に近い程伝播速度が小さくなっている．このため，算定される伝播速度は地震計が埋設された深さまでの平均的な速度である．また方位角は，特に鉛直との角度は，地表に近づく程一般に減少する（鉛直方向に近づく）ものと考えられ，算定される方位角も平均的な方位角であると考えられる．ただし，「平均的な」とは単純な平均値ではなく，地震計の深さ毎の個数の違いなどに影響を受ける平均値である．

（続き）